Non-Equilibrium Mechanics Laboratory




Click on an ongoing or past research thrust to learn more!

Data-driven approaches to modeling non-equilibrium phenomena.
We strive to incorporate thermodynamics and statistical physics into our data-driven approaches so as to learn thermodynamically consistent models and uniquely extract important material information from the dynamics.
-
Variational learning strategy for the discovery of non-equilibrium equations, through the variational action density from which these equations may be derived. The strategy is based on the so-called Onsager’s variational principle, which may be written as a function of the free energy and dissipation potential, and utilizes neural network architectures that strongly guarantee thermodynamic consistency.
Publications:
- S. Huang, Z. He, B. Chem and C. Reina. Variational Onsager Neural Networks (VONNs): A thermodynamics-based variational learning strategy for non-equilibrium PDEs. Journal of the Mechanics and Physics of Solids 163 (2022): 104856. [web].
-
Simulatneous discovery of the internal variables needed to describe the system's evolution in a Markovian fashion.
Publications:
- W. Qiu, S. Huang and C. Reina. Bridging statistical mechanics and thermodynamics away fromequilibrium: a data-driven approach for learning internal variables and their dynamics. Journal of the Mechanics and Physics of Solids, 203, 106211 (2025). [web]
-
Physics-based data-driven approaches for the discovery of continuum equations. Here, we leverage infinite dimensional fluctuation-dissipation relations and fluctuation theorems valid far away from equilibrium to fully learn from data the PDEs governing the system's evolution, and uniquely characterize the free energy and the kinetics. We note that dynamics themselves do not uniquely provide such information.
Publications:
- S. Huang, Z. He, N. Dirr, J. Zimmer, and C. Reina. Statistical-Physics-Informed Neural Networks (Stat-PINNs): A Machine Learning Strategy for Coarse-graining Dissipative Dynamics. Journal of the Mechanics and Physics of Solids, 194, 105908 (2025). [web]
- S. Huang, C. Sun, P. K. Purohit and C. Reina. Harnessing fluctuation theorems to discover free energy and dissipation potentials from non-equilibrium data. Journal of the Mechanics and Physics of Solids (2021): 104323. [web]
- X. Li, N. Dirr, P. Embacher, J. Zimmer and C. Reina. Harnessing fluctuations to discover dissipative evolution equations. Journal of the Mechanics and Physics of Solids, 131 (2019): 240-251. [web]
- P. Embacher, N. Dirr, J. Zimmer, C. Reina. Computing diffusivities from particle models out of equilibrium. Proceedings of the Royal Society A, 474 (2018): 220170694. [web]
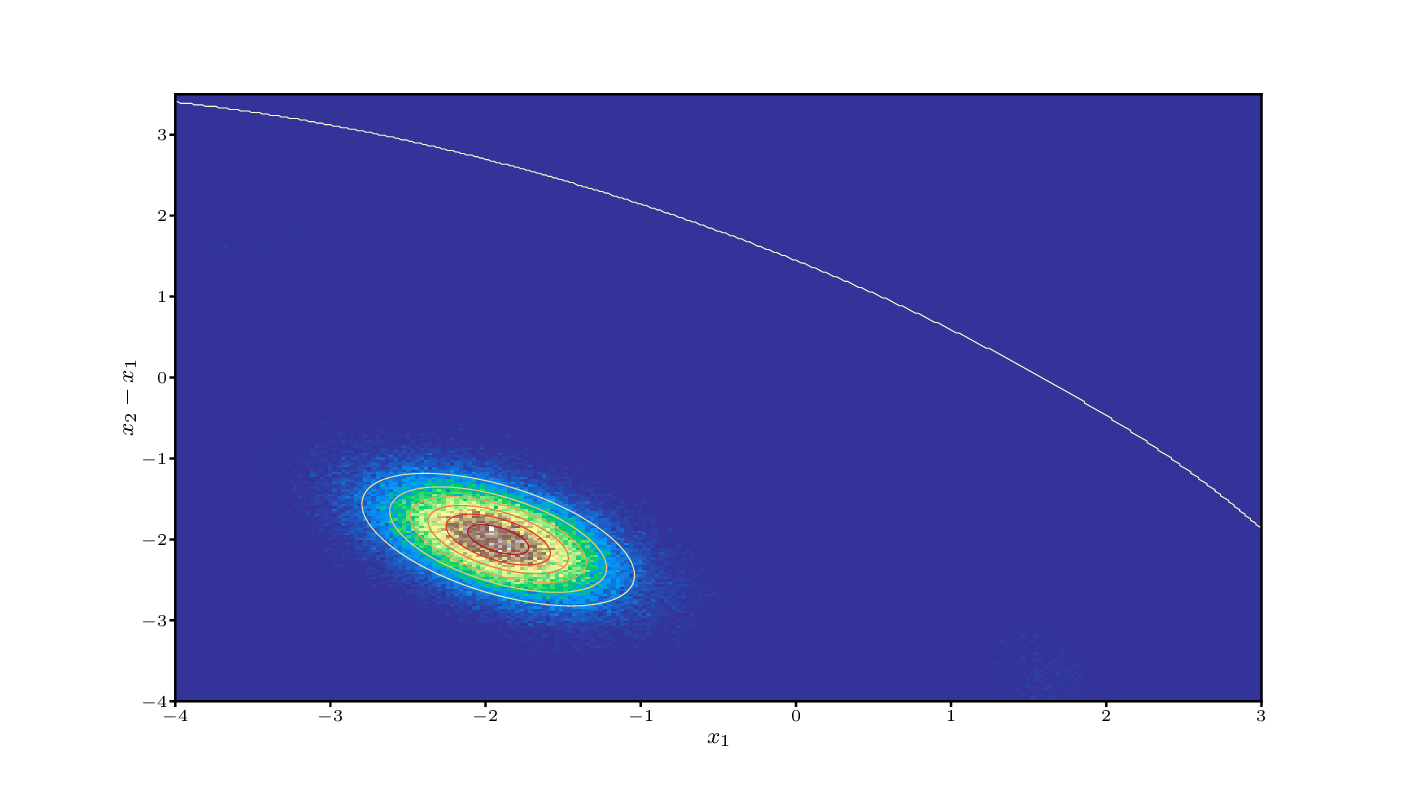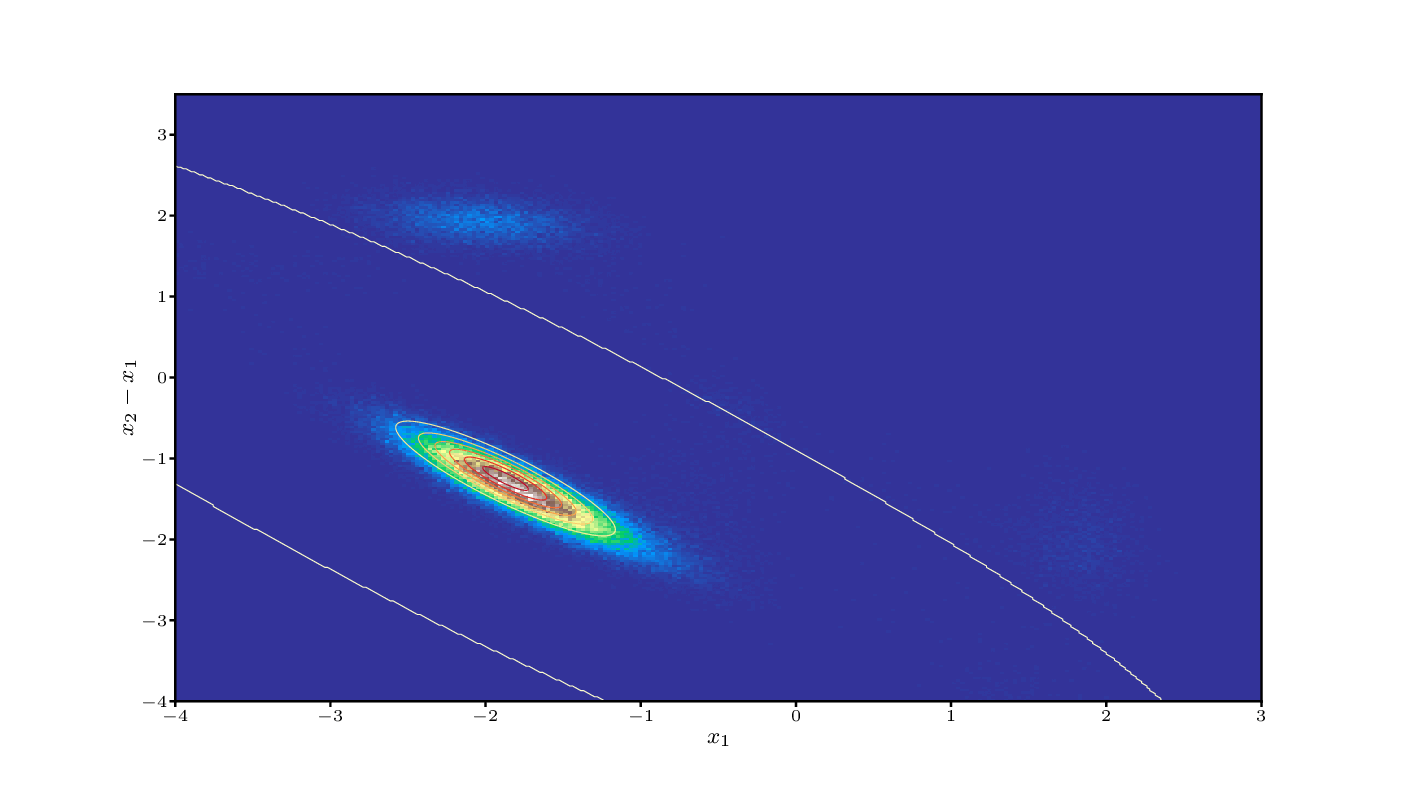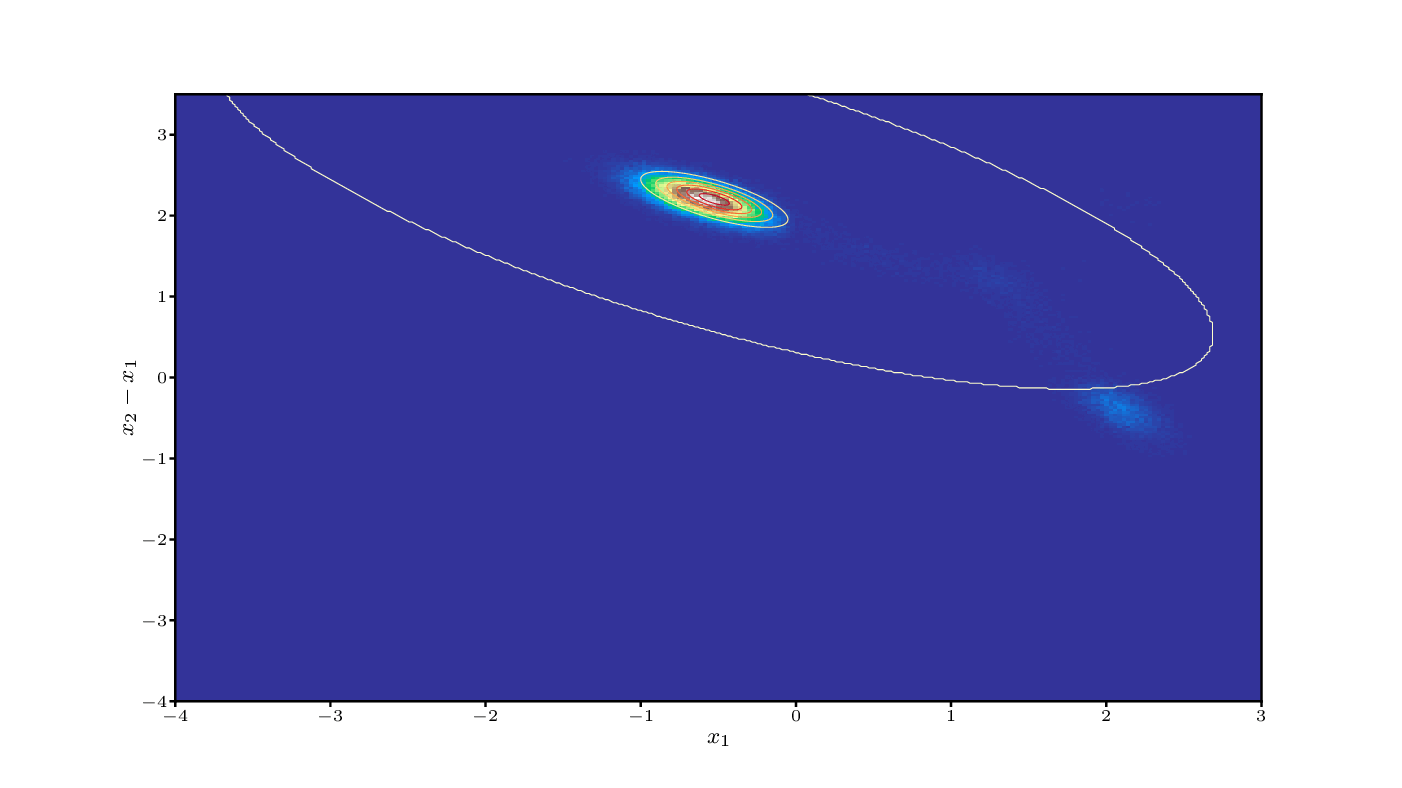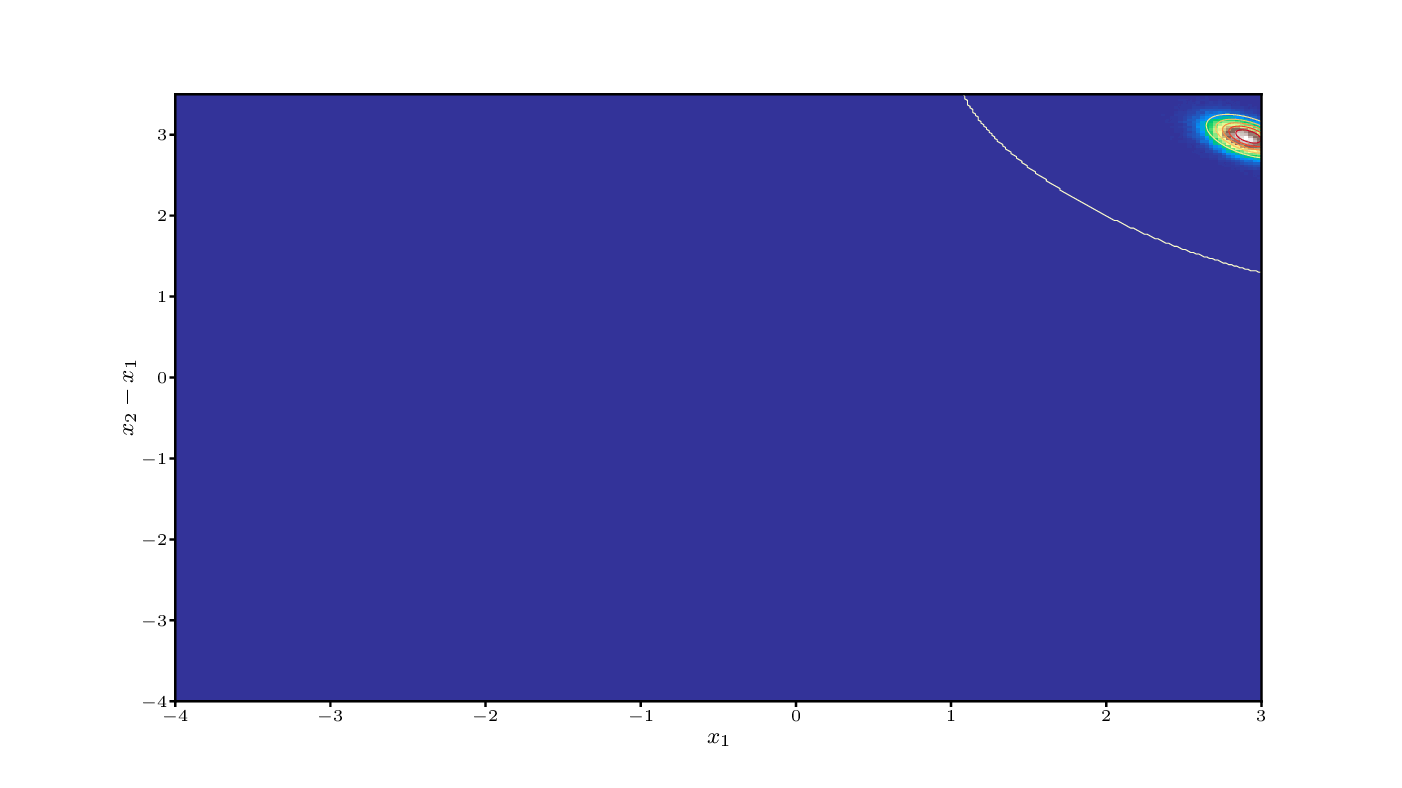
Non-equilibrium statistical mechanics
We have developed a statistical mechanics framework for far-from equilibrium phenomena that delivers continuum thermodynamic models with internal variables from particle systems governed by Langevin dynamics in the absence of any fitting to experiments or lower-scale simulations.
-
The framework is called Stochastic Thermodynamics with Internal Variables (STIV). It is built upon three ingredients: (a) a parametric approximation of the probability distribution, where the parameters are the internal variables, (b) stochastic thermodynamics for the definition of all thermodynamic potentials away from equilibrium, and (c) a variational method of Eyink to obtain the evolution equations for the internal variables.
Publications:
- T. Leadbetter, P. Purohit, and C. Reina. A statistical mechanics framework for constructing non-equilibrium thermodynamic models. Proceedings of the National Academy of Sciences of the United States of America Nexus, 2.12, pgad417, (2023). [web]
-
The framework has allowed us to obtain the first ab-initio derivation of a phase field model for phase transitions in an elastic system.
Publications:
- T. Leadbetter, P. K. Purohit, and C. Reina. A statistical mechanics derivation and implementation of non-conservative phase field models for front propagation in elastic media. Journal of the Mechanics and Physics of Solids, 204, 106240 (2025). [web]

Continuum modeling of non-equilibrium phenomena.
The modeling of dissipative evolution equations remains a major challenge in continuum mechanics and is primarily based on phenomenological constitutive relations. Our efforts in this area are multifaceted and encompass
-
The foundational understanding of the continuum equations of motion and their thermodynamic structure, from systems governed by Hamiltonian dynamics. Here, we observed from data the inherent spatial and temporal scale separation (i.e., the existence of slow and fast degrees of freedom), and show how the reversible or dissipative nature of the system at the continuum scale emerges as a function of that scale separation.
Publications:
- M. Klar, K. Matthies, C. Reina and J. Zimmer. Second-order fast-slow dynamics of non-ergodic Hamiltonian systems: Thermodynamic interpretation and simulation. Physica D: accepted. [arxiv]
- X. Li and C Reina. Simultaneous spatial and temporal coarse-graining: From atomistic models to continuum elastodynamics. Journal of the Mechanics and Physics of Solids, 130 (2019): 118-140. [web]
-
Connections between the geometry of dissipative gradient flows, the principle of maximum entropy production, large deviation principles for stochastically augmented evolution equations and fluctuation-dissipation relations.
Publications:
- C. Reina and J. Zimmer. Entropy production and the geometry of dissipative evolution equations. Physical Review E, 92 (2015): 052117. [web]

Extrapolating material response into the far-from-equilibrium realm
Despite their ubiquity and technological importance, the understanding of far-from-equilibrium material behavior remains at its infancy. Here, we propose a strategy to extrapolate material behavior with quantified uncertainty to distinct loading conditions or material systems. This includes, as a specific example, the prediction of the far-from-equilibrium behavior from equilibrium trajectory data, like the emergence of caging in glass-formers from the liquid phase.
Publications:
- S. Huang, I. R. Graham, R. A. Riggleman, P. Arratia, S. Fitzgerald, and C. Reina. Predicting the unobserved: a statistical mechanics framework for non-equilibrium material response with quantified uncertainty. Journal of the Mechanics and Physics of Solids, (2022): 104779. [web]

Kinematics of finite elastoplasticity.
The kinematic description of large elastoplastic deformations was conjectured in the 1950's to be of the form F=FeFp, where the total deformation F is decomposed multiplicatively into its elastic (Fe) and plastic (Fp) contributions. It has since then become a standard assumption in the continuum modeling of elastoplasticity, as well as general inelastic phenomena, including growth, damage, viscoelasticity, thermoelasticity and phase transformations. However, the absence of a rigorous justification for this decomposition has lead to numerous debates and controversies. Here, we use tools from the calculus of variations to perform rigorous multiscale analyses from discrete dislocations to a continuum formulation and make precise the necessary and sufficient conditions for the validity of F=FeFp (or F=FeFi in the general inelastic setting).
Publications:
- C. Reina, L. F. Djodom, M. Ortiz and S. Conti. Kinematics of elasto-plasticity: Validity and limits of applicability of F= FeFp for general three-dimensional deformations. Journal of the Mechanics and Physics of Solids, 121 (2018): 99-113. [web]
- C. Reina and S. Conti. Incompressible inelasticity as an essential ingredient for the validity of the kinematic decomposition F=FeFi. Journal of the Mechanics and Physics of Solids, 107 (2017): 322-342. [web]
- C. Reina, A. Schlomerkemper and S. Conti. Derivation of F=FeFp as the continuum limit of crystalline slip. Journal of the Mechanics and Physics of Solids, 89 (2016): 231-254. [web]
- C. Reina and S. Conti. Kinematic description of crystal plasticity in the finite kinematic framework: a micromechanical understanding of F=FeFp. Journal of the Mechanics and Physics of Solids, 67 (2014): 40-61. [web]

Design of elastic metamaterials.
Internal resonances are widely used in elastic metamaterials to generate subwavelength bandgaps, where no waves propagate. However, these bandgaps tend to be very narrow, severely limiting their applicability. Drawing inspiration from biological materials, we have explored the role of hierarchical architectures and softness as important and rich mechanisms for bandgap widening. Jointly with the group of Prof. Raney, we have fabricated an additively manufactured soft resonant metamaterial with a gap-midgap ratio of 81.8%, greatly surpassing metamaterials of the same class found in the literature.
Publications:
- B. Chem, Y. Jian, C. Liu, J. R. Raney and C. Reina. Dynamic behavior of soft resonant metamaterials: experiments and simulations. Journal of Applied Physics, 129 (2021): 135104. [web]
- C. Liu, C. Reina. Broadband locally resonant metamaterials with graded hierarchical architecture. Journal of Applied Physics, 123 (2018): 095108. [web]

Computational homogenization for elastic wave propagation.
Computational multiscale techniques, such as FE2 methods, take advantage of the separation of length scales to deliver efficient numerical strategies capable of capturing both the local and effective material behavior. They were originally developed for the quasi-static setting based on micro-to-macro relations that enable the appropriate coupling between the two different scales. Here, we extend these relations to the discrete and dynamic setting to simulate wave propagation in dispersive media at a reduced computational cost.
Publications:
- C. Liu, C. Reina. Dynamic homogenization of resonant elastic metamaterials with space/time modulation. Computational Mechanics, 64.1 (2019): 147-161. [web]
- C. Liu, C. Reina. Variational coarse-graining procedure for dynamic homogenization. Journal of the Mechanics and Physics of Solids, 104 (2017): 187-206. [web]
- C. Liu, C. Reina. Discrete averaging relations for micro to macro transition. Journal of Applied Mechanics, 83-8 (2016): 081006. [web]

Modeling of amorphous-to-crystalline transformation.
Phase change materials (PCMs) can exhibit ultrafast phase transformations and are considered as promising candidates for non-volatile memory devices. Yet, a full understanding of this non-equilibrium process is still lacking. Here, we develop a thermodynamically consistent atomistic-phase field models for the understanding of the nano-crystallization of amorphous Ge, a base element of many PCMs.
Publications:
- L. Sandoval, C. Reina and J. Marian. Formation of Nanotwin Networks during High-Temperature Crystallization of Amorphous Germanium. Scientific Reports, 5 (2015): 17251. [web]
- C. Reina, L. Sandoval and J. Marian. Mesoscale computational study of the nano-crystallization of amorphous Ge via a self-consistent atomistic - phase field model. Acta Materialia, 77 (2014): 335-351. [web]

Damage via void nucleation and growth.
Damage and failure by voids occur in a wide range of materials ranging from biological tissue to polymers and metals. We have developed multiscale models and simulations that transfer information all the way from the quantum level to the continuum scale using kinetic Monte Carlo methods, multiscale finite element techniques and estimates from quasi-continuum simulations.
Publications:
- C. Reina, B. Li, K. Weinberg and M. Ortiz. A micromechanical model of distributed damage due to void growth in general materials and under general deformation histories. International Journal for Numerical Methods in Engineering, 93 (2013): 575-611. [web]
- C. Reina, J. Marian and M. Ortiz. Nanovoid nucleation by vacancy aggregation and vacancy-cluster coarsening in high-purity metallic single crystals. Physical Review B, 84 (2011): 104117. [web]